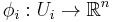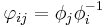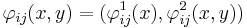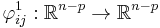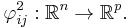Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension.
Contents |
Definition
More formally, a dimension  foliation
foliation  of an
of an  -dimensional manifold
-dimensional manifold  is a covering by charts
is a covering by charts 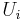 together with maps
together with maps
such that on the overlaps 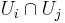 the transition functions
the transition functions 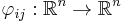 defined by
defined by
take the form
where  denotes the first
denotes the first 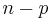 coordinates, and
coordinates, and  denotes the last p co-ordinates. That is,
denotes the last p co-ordinates. That is,
and
In the chart 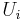 , the stripes
, the stripes 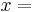 constant match up with the stripes on other charts
constant match up with the stripes on other charts 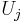 . Technically, these stripes are called plaques of the foliation. In each chart, the plaques are
. Technically, these stripes are called plaques of the foliation. In each chart, the plaques are  dimensional submanifolds. These submanifolds piece together from chart to chart to form maximal connected injectively immersed submanifolds called the leaves of the foliation.
dimensional submanifolds. These submanifolds piece together from chart to chart to form maximal connected injectively immersed submanifolds called the leaves of the foliation.
The notion of leaves allows for a more intuitive way of thinking about a foliation. A  -dimensional foliation of a
-dimensional foliation of a  -manifold
-manifold  may be thought of as simply a collection
may be thought of as simply a collection 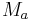 of pairwise-disjoint, connected
of pairwise-disjoint, connected  -dimensional sub-manifolds (the leaves of the foliation) of
-dimensional sub-manifolds (the leaves of the foliation) of  , such that for every point
, such that for every point  in
in  , there is a chart
, there is a chart 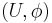 with
with  homeomorphic to
homeomorphic to 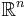 containing
containing  such that for every leaf
such that for every leaf 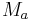 ,
, 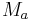 meets
meets  in either the empty set or a countable collection of subspaces whose images in
in either the empty set or a countable collection of subspaces whose images in 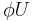 are
are  -dimensional affine subspaces whose first
-dimensional affine subspaces whose first 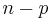 coordinates are constant.
coordinates are constant.
If we shrink the chart 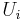 it can be written in the form
it can be written in the form 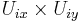 where
where
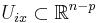 and
and 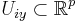 and
and 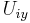
is isomorphic to the plaques and the points of 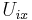 parametrize the plaques in
parametrize the plaques in 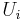 . If we pick a
. If we pick a
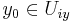 ,
, 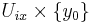
is a submanifold of 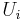 that intersects every plaque exactly once. This is called a local transversal section of the foliation. Note that due to monodromy there might not exist global transversal sections of the foliation.
that intersects every plaque exactly once. This is called a local transversal section of the foliation. Note that due to monodromy there might not exist global transversal sections of the foliation.
Examples
Flat space
Consider an  -dimensional space, foliated as a product by subspaces consisting of points whose first
-dimensional space, foliated as a product by subspaces consisting of points whose first 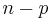 co-ordinates are constant. This can be covered with a single chart. The statement is essentially that
co-ordinates are constant. This can be covered with a single chart. The statement is essentially that
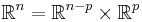
with the leaves or plaques 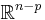 being enumerated by
being enumerated by 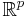 . The analogy is seen directly in three dimensions, by taking
. The analogy is seen directly in three dimensions, by taking 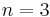 and
and 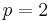 : the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.
: the two-dimensional leaves of a book are enumerated by a (one-dimensional) page number.
Covers
If 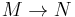 is a covering between manifolds, and
is a covering between manifolds, and  is a foliation on
is a foliation on  , then it pulls back to a foliation on
, then it pulls back to a foliation on  . More generally, if the map is merely a branched covering, where the branch locus is transverse to the foliation, then the foliation can be pulled back.
. More generally, if the map is merely a branched covering, where the branch locus is transverse to the foliation, then the foliation can be pulled back.
Submersions
If 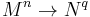 (where
(where 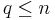 ) is a submersion of manifolds, it follows from the inverse function theorem that the connected components of the fibers of the submersion define a codimension
) is a submersion of manifolds, it follows from the inverse function theorem that the connected components of the fibers of the submersion define a codimension  foliation of
foliation of  . Fiber bundles are an example of this type.
. Fiber bundles are an example of this type.
Lie groups
If  is a Lie group, and
is a Lie group, and  is a subgroup obtained by exponentiating a closed subalgebra of the Lie algebra of
is a subgroup obtained by exponentiating a closed subalgebra of the Lie algebra of  , then
, then  is foliated by cosets of
is foliated by cosets of  .
.
Lie group actions
Let  be a Lie group acting smoothly on a manifold
be a Lie group acting smoothly on a manifold  . If the action is a locally free action or free action, then the orbits of
. If the action is a locally free action or free action, then the orbits of  define a foliation of
define a foliation of  .
.
Kronecker foliation
The set of lines on the torus T = R2/Z2 with the same slope θ forms a foliation. The leaves are obtained by projecting straight lines of slope θ in the plane R2 onto the torus. If the slope is rational then all leaves are closed curves homeomorphic to the circle, while if it is irrational, the leaves are noncompact, homeomorphic to the real line, and dense in the torus (cf Irrational rotation). The irrational case is known as the Kronecker foliation, after Leopold Kronecker. A similar construction using a foliation of Rn by parallel lines yields a one-dimensional foliation of the n-torus Rn/Zn associated with the linear flow on the torus.
Foliations and integrability
There is a close relationship, assuming everything is smooth, with vector fields: given a vector field  on
on  that is never zero, its integral curves will give a 1-dimensional foliation. (i.e. a codimension
that is never zero, its integral curves will give a 1-dimensional foliation. (i.e. a codimension 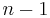 foliation).
foliation).
This observation generalises to the Frobenius theorem, saying that the necessary and sufficient conditions for a distribution (i.e. an 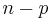 dimensional subbundle of the tangent bundle of a manifold) to be tangent to the leaves of a foliation, is that the set of vector fields tangent to the distribution are closed under Lie bracket. One can also phrase this differently, as a question of reduction of the structure group of the tangent bundle from
dimensional subbundle of the tangent bundle of a manifold) to be tangent to the leaves of a foliation, is that the set of vector fields tangent to the distribution are closed under Lie bracket. One can also phrase this differently, as a question of reduction of the structure group of the tangent bundle from 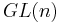 to a reducible subgroup.
to a reducible subgroup.
The conditions in the Frobenius theorem appear as integrability conditions; and the assertion is that if those are fulfilled the reduction can take place because local transition functions with the required block structure exist. For example, in the codimension 1 case, we can define the tangent bundle of the foliation as 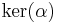 , for some (non-canonical)
, for some (non-canonical) 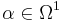 (ie a non-zero co-vector field). A given
(ie a non-zero co-vector field). A given  is integrable iff
is integrable iff 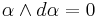 everywhere.
everywhere.
There is a global foliation theory, because topological constraints exist. For example in the surface case, an everywhere non-zero vector field can exist on an orientable compact surface only for the torus. This is a consequence of the Poincaré–Hopf index theorem, which shows the Euler characteristic will have to be 0. There are many deep connections with contact topology, which is the "opposite" concept.
Existence of foliations
Haefliger (1970) gave a necessary and sufficient condition for a distribution on a connected non-compact manifold to be homotopic to an integrable distribution. Thurston (1974, 1976) showed that any compact manifold with a distribution has a foliation of the same dimension.
See also
- G-structure
- Classifying space for foliations
- Haefliger structure, a generalization of foliations closed under taking pullbacks.
- Lamination
- Reeb foliation of the 3-sphere.
- Taut foliation
References
- Anosov, D.V. (2001), "Foliation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=F/f040740
- Haefliger, André (1970), "Feuilletages sur les variétés ouvertes", Topology. an International Journal of Mathematics 9 (2): 183–194, doi:10.1016/0040-9383(70)90040-6, ISSN 0040-9383, MR0263104
- Lawson, H. Blaine (1974), "Foliations", Bulletin of the American Mathematical Society 80 (3): 369–418, doi:10.1090/S0002-9904-1974-13432-4, ISSN 0002-9904, MR0343289, http://www.ams.org/bull/1974-80-03/S0002-9904-1974-13432-4/
- Moerdijk, Ieke; Mrčun, J. (2003), Introduction to foliations and Lie groupoids, Cambridge Studies in Advanced Mathematics, 91, Cambridge University Press, ISBN 978-0-521-83197-0, MR2012261
- Reeb, Georges (1952), Sur certaines propriétés topologiques des variétés feuilletées, Actualités Sci. Ind., no. 1183, Hermann & Cie., Paris, MR0055692
- Thurston, William (1974), "The theory of foliations of codimension greater than one", Commentarii Mathematici Helvetici 49: 214–231, doi:10.1007/BF02566730, ISSN 0010-2571, MR0370619, http://gdz.sub.uni-goettingen.de/no_cache/en/dms/load/img/?IDDOC=213742
- Thurston, William P. (1976), "Existence of codimension-one foliations", Annals of Mathematics. Second Series (Annals of Mathematics) 104 (2): 249–268, doi:10.2307/1971047, ISSN 0003-486X, JSTOR 1971047, MR0425985